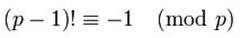A WAY TO UNDERSTAD PRIMES:

A WAY TO UNDERSTAD PRIMES:

by Stefano Maruelli – Read & check, at your own risk !

Powers and Factorial:

Last Update 20-04-2013

A WAY TO UNDERSTAD PRIMES:

Probably due to the “Primes mito” many articles and books forgot that before talk about primes is necessary to understand some think on primes that comes directly from the definition so:

1- How to discover if n is a prime

2- How to discover the position of any primes in the primes list

3- How to find the next prime

1- How to discover if n is a prime:

From primes definition I discover (but was probably known from all mathematician from 1700d.c.) that using the “z” fraction:

be “n” an integer >= 5

if we calculate Rm: as following, we found that (! = Factorial):

| - an integer than n <> prime

(1) z = n! / n^2 = |

| - rational (from 24/5) than n = prime

Unfortunately this method show in few numbers how .XLS or similar non math programs are “limited” in the calculation of big numbers like n!.

Pari GP can help you lot.

What is interesting (that can be seen also in XLS table till 17, only) is that:

the non integer part of z, in case of n= prime

start from 0.8 (or 24/5) and goes to 0.9999…. for z= (infinite-1) ! / infinite

So prime has a very interesting property that allow us to recognize them immediately, and count them immediately (if we hold a supercomputer….)

1b- Connection to Wilson Theorem:

The not so simple form of this function (called Wilson theorem) is:

Descrizione: wilkinson1

2- How to discover the position of any primes in the primes list

With this simple trick you can understand the position of the primes “n” in the primes table or how many primes there where before the integer “n”:

The official formula is:

Descrizione: wilkinson2

Where { X } is the non integer part of X, forced as 1

A more simple to understand method is:

- Force to 0 the integer part of Rm

- force at 1 the non integer part of the Rm value

So in case “n” is a prime it count 1, or 0 in case of non prime, so the sum from 1 to n will return exactly the number of the primes.

Since the method start from 5 we have to add 2 to remember of:

2= prime and 3= prime, missed starting from 5:

Descrizione: Stefano%20Maruelli%20the%20number%20of%20prime%20before%20P%20formulazzen

(0.3 pull decimal to 1 in case n is a prime, 2 )

Here the LaTeX formula:

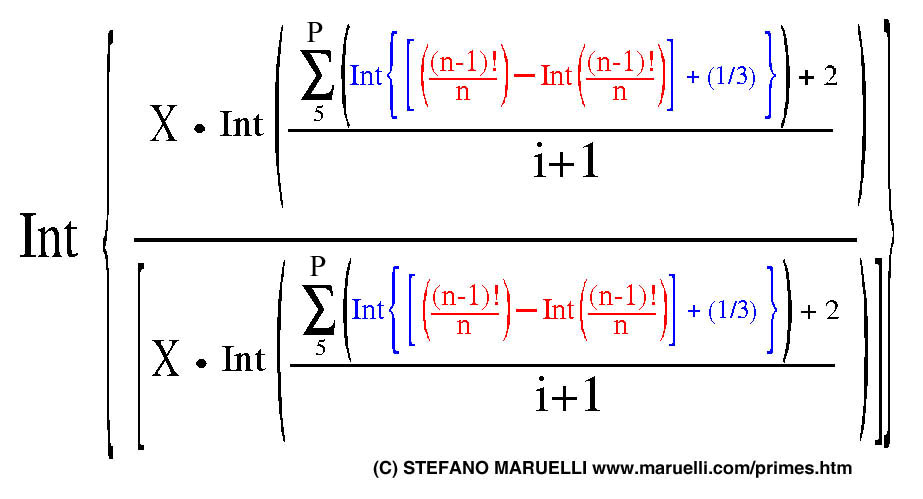
{tex} Pi(x) = \sum_{n = 5}^{\ P}{ [Int [[((n!/n^2)-int(n!/n^2)]+0.3]] +2 } {/tex}

3- How to find the next prime:

With the similar method is possible to answer at the question:

If, for example be Pi(a) = 31 is a known prime, witch is the next prime ?

The process is the same:

- calculate the position “i” of the known “Pi” with the method (2) :

so Pos(31) = i than Pos(Pi+1)= (i+1)

- than knowing that the new position (i+1) will be “easy” to

- calculate the relative prime

One of the possible the tricks is:

- Knowing that P * 0 = 0 find a way to force at zero any number that has a position different from (a+1)

so first step is to calculate:

Descrizione: Stefano%20Maruelli%20the%20next%20prime%20step2

This give as result:

- 0 if n < P(i+1)

- 1 if n = P(i+1)

- K if n = P(i+K)

So we have to find a tricks that gives 0 or 1 still if n = P(i+K) and avoid the indeterminate form 0/0.

For example we know that b! = 1 still if b = 0 so: int( b/b! ) avoid the form 0/0

And return 1 if b=1 since if b =1 also b! = 1! = 1. So we use the:

Descrizione: Stefano%20Maruelli%20the%20next%20prime%20step3

This give as result:

- 0 if n <> P(i+1)

- 1 if n = P(i+1)

So to make it working itself we can put this trick into a Sum that works from known limits where Pi(i+1) will be for sure present.

For example lower limit is: P(i)+1 and upper is: 2* Pi (as already proven see wikipedia)

Of course the tricks works with the upper limit till infinite, but has no sense.

So the “final trick” to have the P(i+1) knowing Pi is:

Descrizione: Stefano%20Maruelli%20the%20next%20prime%20formulazzen

All that works as a very slow computer program, so has no sense for make a real calculation, but can give you an idea of what make Primes soo hard to be discovered.

So is necessary to “process” all the numbers from 5 to X each time, and for several times…)

But we cannot say longer that “is impossible to find a formula to calculate the next prime”.

And finally we azzard to say that seems now more probable that there will not be an absolutely easy function that feet all primes.

Of course there are other more faster algorithm to find primes (for example Eartostene method) but, in my opinion, they will not give a “sense” of how prime are made as Wilkinson theorem (and what follow from it).

There is non official formula discovered in 1964 that involves sin(x) and Integer operator too.

4- My final concerning on:

I try to go over saying that is more clear now why complex numbers can well fit the primes calculation:

complex numbers, as primes, has 2 non connected “parts”:

the real one and the complex,

as prime can be connected to a number z = n!/n^2 that has

an integer part, that is common to a non primes numbers,

and a non integer part that is unique and non present in non primes numbers.

Complicate Modulus Algebra

Solve the n-root by hand, and Fermat too !

A new story ?

Power of integers properties to