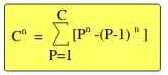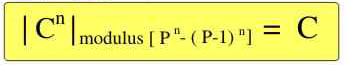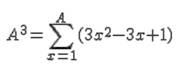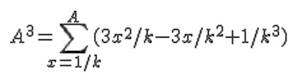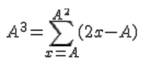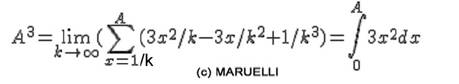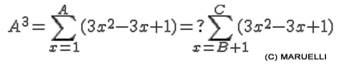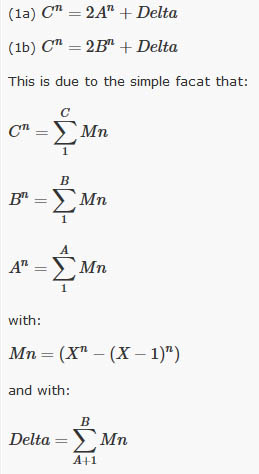Complicate Modulus Algebra (daily rev. on news)

by Stefano Maruelli – Read & check, at your own risk !

Complicate Modulus Algebra

Solve the n-root by hand, and Fermat too !

A new story ?

A day walking with my wife, I ask her if is known a “special” modular algebra where the modulus is not just a number, but a function... Since I’ven’t found nothink on that I wrote here my concerning on.

2016-11-15 New: Read all the story of an easy instruments to solve n-th problems like Fermat the last & Beal:

The Two Hands Clock

Since on the first linked PDF there is the last available Draft on Fermat The Last, I'm working to clean-up, asap, this PDF to left just the part regerdin the Sum Properties and the Beal Problem

For thoos would like to have a short preview of what into the pdf you can read here...

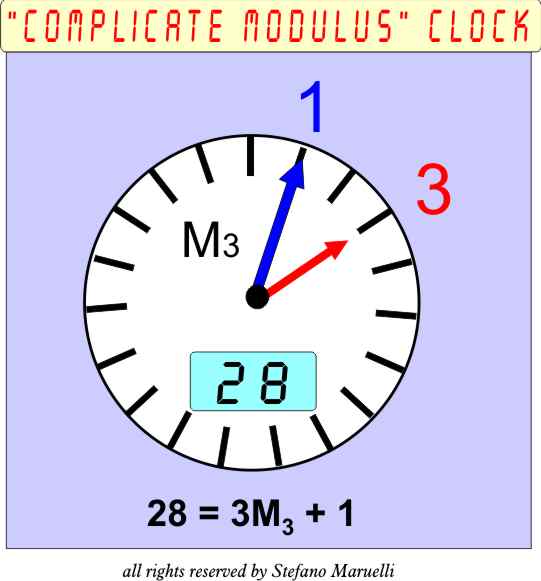
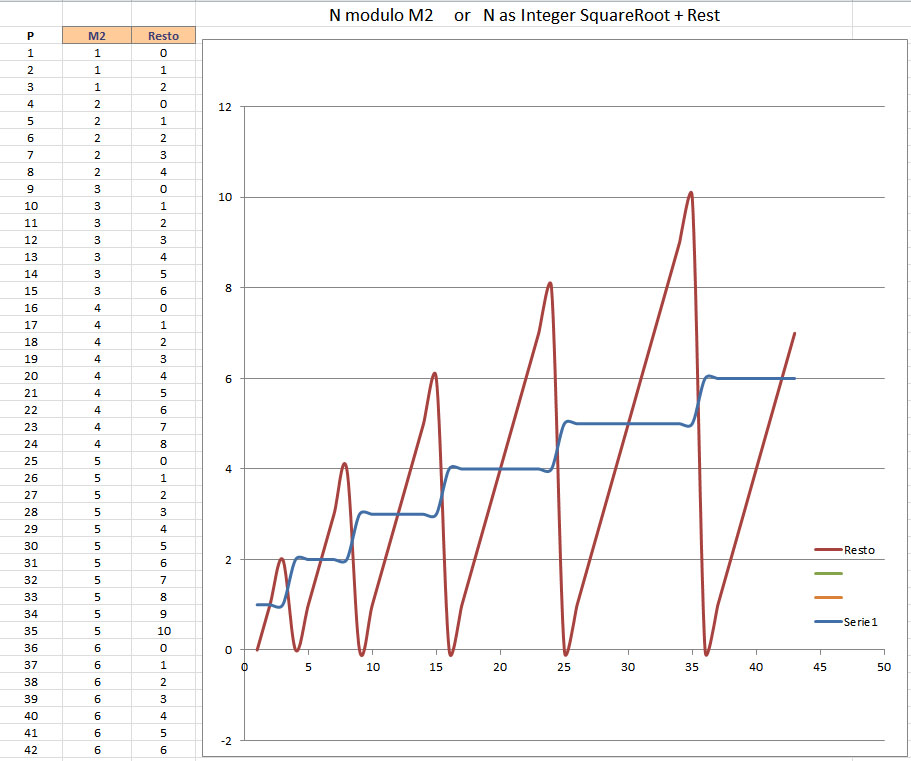
PART 1) THE "COMPLICATE MODULUS" ( DEFINITION)

- What "complicate modulus" algebra is:

- Is a clock (or better a special counter) with 2 hands: one is the numbers of turn ( for example called with "m" extension) the other is the rest "R".

Also it's special since the numbers of hours (reference line) onto the clock, change at each turn of a known function called  "complicate modulus, M(n)".

So also the reference lines are not printed, but displayed as digital line that divide the circle.

We can also imagine a more complicate, or complex, counter, based on the same model...

- A simple example of  how powerful is the "complicate modulus" algebra:

EXAMPLE: CONSIDERING POWERS OF INTEGERS:

All was born studying Fermat the Last with my poor math. instruments.

I understood that we can develop any power of integer as:

We call   M(n) = [ Pⁿ  - ( P-1) ⁿ ] "complicate modulus" since:

We prove that this can be an easy method to extract the "n" root by hand (or just to understand if an integer "N" is a perfect power "n")

For example for n=3 we have that the cube A^3 cab be written as:

PART 2) INVOLVING TARTAGLIA'S TRIANGLE

It helps us to understand what is, and the values, of our "complicate modulus" operator since:

« Complicate modulus » M(n) = [ Pⁿ  - ( P-1) ⁿ ] 

So to obtain it (mnemonic rules), is enough to:

a)  Keep the Tartaglia's (x-1)^n develop interested (n-th) line,  

b)  Remove the first value (that is ever "1") and

c) Change all the sign

d) Write the resulting line into the sum from 1 to A.

Example:

Remembering the triangle (calculated for x-1) considering the value with sign :

Power	TARTAGLIA’S (x-1)^n	Check Sum dig.	Our Complicate Modulus formula	Complicate Modulus Value:
0	1
1	1-1	0
2	1-2+1	0	M2 =  [X^2-(X-1)^2]	M2 =  2x-1
3	1 -3+3-1	0	M3 = [X^3-(X-1)^3]	M3 = 3x^2- 3x +1
4	1-4  6 -4  1	0	M4 =  [X^4-(X-1)^4]	M4 =4x^3-6x^2+4x - 1
Etc…

PART 3) HOW TO CALCULATE BY HAND "n" ROOT: 

If we wanna know if an integer "m" has an integer (n) root

Exampe:

We would like to calculate by hands the square root of m =  9:

So we first  wrote Tartaglia's line for (x-1)  and n=2:

1 -2  1

we remove the first value

 -2 1

we change the signs a re-put the x value (with their powers) then we obtain our M2 modulus :

  M2=  2x-1  

So we can easlily tabulate (and calculate the square root):

x	2x-1	Value= 9	Rest
1	1	9-1=	8
2	3	8-3=	5
3	5	5-5=	0

So Rest = 0 than end of calculation. Result:  9 is a perfect square !

Or:   | 9 | M2 = 3 M2 + 0

The “fact” that “sum of all odds” is ever a square was well known.

What I don't see any ware is that in the same way we can calculate each n power using the "complicate modulus operator".

Also is evident, but, was not soo clear to me before experience on that, that is possible to "reverse" the calculation to obtain the square root.

Example for n=3 ,   cubic root by hand:

We  have, for example the number  "28" and we would like it as an integer bubic root and witch is.

From Tartaglia, line n=3  for (x-1)³

n= 3      1 -3+3-1             we remove the first having:

  -3+3-1 and we change the sign so:

  M3 = [X³-(X-1)³]  = 3x²- 3x +1

And we can calculate:

x	(3x^2 -3x+1)	Value= 28	Rest
1	1	28-1 =	27
2	7	27-7  =	20
3	19	20-19  =	1

 So 28 has no perfect cubic root or:

| 28 | [M3=(3x² - 3x +1)] = 3M3 + 1

ETC...... So we are now able to make any (n) root...

PART 4) New M(n) simbols, some examples: 

How to write the "complicate modulus "result: (sorry probably I invent the hot water ?)

   27 modulus M3 = 3 M3+ 0  or

| 27| [M3= (3x²- 3x +1)] =   3 M3 + 0  = 3³ +0

Or as in the final shorter form:

 | 30| M₃  =  3 M₃ + 3  = 3³ + 3

 | 625| M₄ =  5 M₄ + 0  

 | 627| M₄ =  5 M₄ + 2   etc....

We leave M(n) simbol into the result to clarify what we did.

All this comes from the Binomial develop rules of (x-1)^n

All this concerning can be also done using the Binomial develop rules of:

A^n= (x-z)^n

Introducing a new Step Sum:

(this is a sum from 1/k step z = 1/k to A)

The Step Sum, to respect the binomial develop has to comply that rules:

1) Start from Lower limit z that is also the Step of the sum (so 1 is a special case of this sum)

2) Ends, to have an integer power, at “A”

3) Lower limit and step Z can be z=1/k at the conditions that k divide exactly A

4) In a special case the lower limit can be >1 but to be a power it can just be A, or A^m and in that case the upper limit must be adjusted in function of the power we are considering.

In this case the addendum term must be kept from upper row of Tartaglia’s triangle, here an example for A^3, and a step sum that start from A and ends at A^2:

this is a basic point to understand the FLT Proof that will follow.

PART 5) Complicate modulus “Mn” can be also used to obtain the n-th root of a non power if instead of a Sun we use a recursive difference method:

1) If we wanna make the square root of A, with 1/10 precision (so 1 digit after the point),

remembering that M2 =2x-1 we have to keep z=1/10 so:

M2, Z = M2/10 = 2zx –z = 2x/10 – 1/100

Plotting the sum Mn/10 from x= 0.1 to x=A step 0.1

we can have A^2,

or vice versa subtracting from: A^2 the term: 2x/10 – 1/100 (for x=1,2,3….A)

we easy obtain the square root of A^2 with 1 digit precision (etc…)

2) If we keep M2/100 = 2x/100 – 1/100^2

we can have the square root till the 2th decimal etc…

3) Same if we keep: M3/10= 3x^2/10 -3x/100 + 1/1000

And we plot from 0.1 to A step 0.1 we can have the cubic root of A^3 with 1 digit precision etc…

This can be useful at Fermat’s era when calculator was not jet invented.

PART 6) From Step Sum, to Fermat’s integral:

Remembering that:

If we keep now precision z=1/k and we look what happen if k goes to infinite:

For example in the case n=3 :

So we, exactly, have the definite integral from 0 to A (with Fermat’s knowledge).

Since ( -3x/ infinite^2) and (1/infinite^3) are null (since of bigger orders)

Where we see the problem that probably stop Fermat in the publication of his results:

How can Fermat’s co-era peoples accept that the infinitesimal number of major order MUST be Not considered ?

For us is, viceversa, simply to wrote and understand the result of that limit.

PART 7) Step Sum with Irrational Steps:

Via Step Sum it's also possible to rise an irrational Upper Limit, under certain conditions. For example it's possible to rise an upper limit that is multiple of 1/2^(1/n) proceeding step 1/(2^(1/n)), or step 1/K*(2^(1/n)).

PART 8) From Complicate Modulus to Fermat’s integral:

PART 9)  Fermat’s the Last, Proof:

Fermat state (not prove) that:

1)

has no integer solution under his conditions: A<B<C integers (co prime if n>2

So we can now re write the (1) as:

(2)

Or we can re-formulate the (1) in the way lead us to the solution:

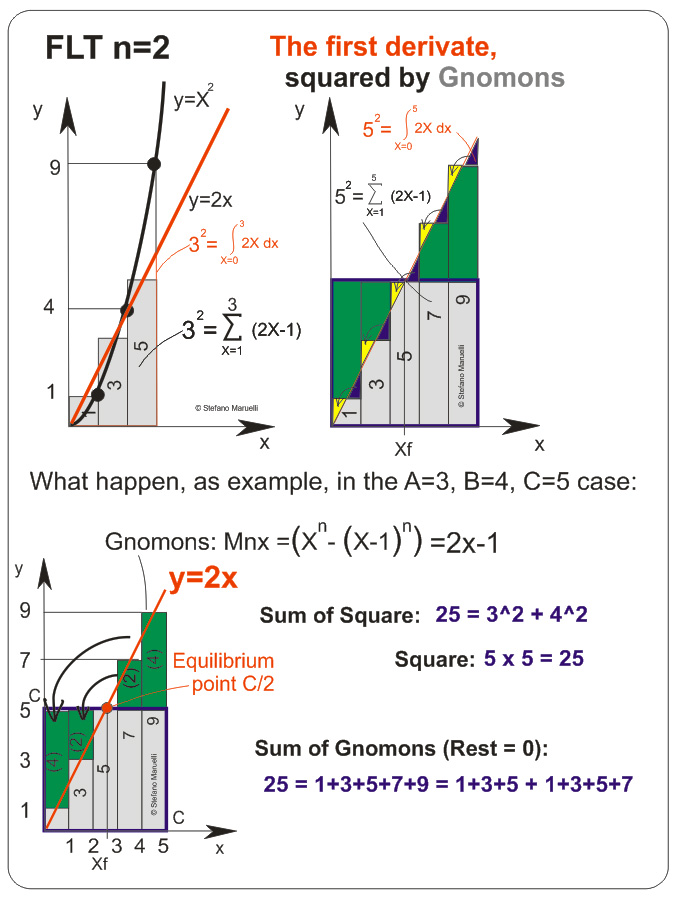
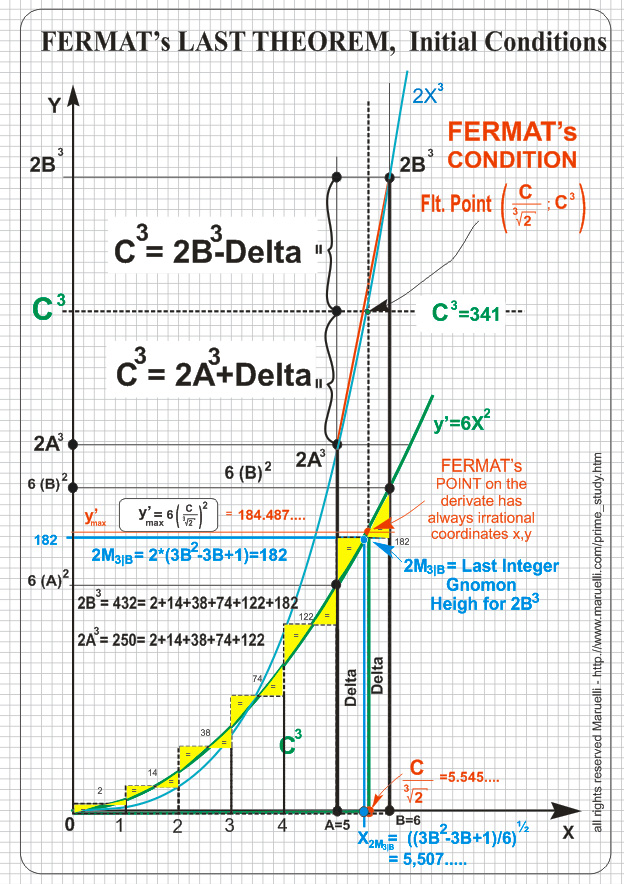
Starting to see what happend in the simple known case n=2:

Whit a linear derivate the Fermat's solution point lives on the derivarte so the exceding gnomon's area on the right perfectly fit the missed left one.

There will be infinite many triplets A,B,C and some different rules to have all them, orto show that for any A there will be minimum one B and one C that will satisfy the equation. Pls read the PDF for more details on.

For bigger "n", taking as example n=3 on the following Graph we can see how Fermat define C^n: (here an example A=5, B=6, n=3)

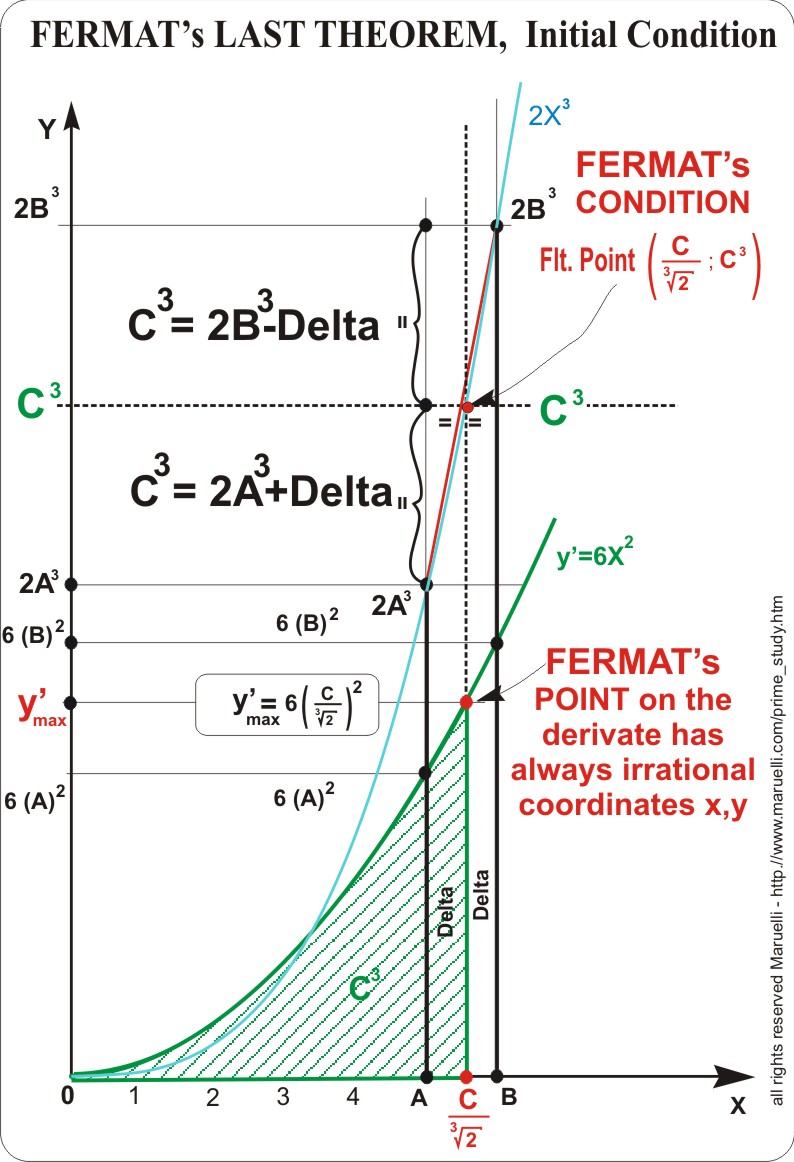
What we can immediately see is that FERMAT define C^n as an height y=C^n that is symmetric respect to 2A^n and 2B^n.

Due to FERMAT's Condition C^n can be defined as THE AREA BELLOW THE DERIVATE till the (always) Irrational value: x = C/(2^(1/n))

I prove it's possible via Step Sum to square an area bellow this derivate till an Integer, Rational or Irrational value (that is the upper limit of the Sum) under certain conditions: the last Step must reach perfectly the Upper limit.

I also prove it's possible to make via Step Sum both Riemann and Lebesgue Integer, Rational, Irrational od Infimus Integration, if we proceed via Step in x, or in y.

As it's immediately clear on the picture FLT Initial condition imply that both on x and y WE HAVE TO RISE AN IRRATIONA UPPER LIMIT, so it gives us no problem if we go infimus with the integral, but IT'S A CLEAR IMPOSSIBLE CONDITION via Irrational Intagration, so via irrational Step Sum because with the Irrational Step it's necessary to reach the Upper limit in X or Y on the derivate that define the area C^n, IT'S NOT POSSIBLE TO PASS BY A and B, when we work in X, nor trough 2nA^(n-1) or 2nB^(n-1) that are INTEGER VALUE BY DEFAULT.

The case n=2 is the only clear possible solution since IS NOT POSSIBLE TO SQUARE THE DERIVATE VIA STEP SUM, but IT'S POSSIBLE VIA TRANGLE AREA FORMULA: b*h/2 and since (n/n-1) it's an integer the product of the two square root of 2 vanish them.

For ALL the others n we have always a NON vanishing product due to Rational Ratio (n/(n-1))

n=2 graph solution asap. (but it's very easy).

Is this the end of 500 years of research of the “elegant” solution ?

I’ve to wait, probably, several years….

Power of integers properties to

Fermat the Last proof

A possible way to Fermat proof using the Complicate Modulus Algebra

Diophantine Equation

How to easily understand integer solutions

Prime study

Solution of n-degree equations